pesawat atwood

PESAWAT ATWOOD

Pesawat atwood adalah alat yang digunakan untuk yang menjelaskan hubungan antara tegangan, energi pontensial dan energi kinetik dengan menggunakan 2 pemberat (massa berbeda) dihubungkan dengan tali pada sebuah katrol. Benda yang yang lebih berat diletakan lebih tinggi posisinya dibanding yang lebih ringan. Jadi benda yang berat akan turun karena gravitasi dan menarik benda yang lebih ringan karena ada tali dan katrol.

Galileo melakukan pengamatan mengenai benda-benda jatuh bebas. Ia menyimpulkan dari pengamatan-pengamatan yang dia lakukan bahwa benda – benda berat jatuh dengan cara yang sama dengan benda-benda ringan. Tiga puluh tahun kemudian, Robert Boyle, dalam sederetan eksperimen yang dimungkinkan oleh pompa vakum barunya, menunjukan bahwa pengamatan ini tepat benar untuk benda-benda jatuh tanpa adanya hambatan dari gesekan udara. Galileo mengetahui bahwa ada pengaruh hambatan udara pada gerak jatuh. Tetapi pernyataannya walaupun mengabaikan hambatan udara, masih cukup sesuai dengan hasil pengukuran dan pengamatannya dibandingkan dengan yang dipercayai orangpada saat itu (tetapi tidak diuji dengan eksperimen) yaitu kesimpulan Aristoteles yang menyatakan bahwa,” Benda yang beratnya sepuluh kali benda lain akan sampai ke tanah sepersepuluh waktu dari waktu benda yang lebih ringan”. Pada tahun 1678 Sir Isaac Newton menyatakan hukum pertamanya tentang gerak, yang sekarang kita kenal sebagai Hukum I Newton Hukum I Newton menyatakan “Sebuah benda akan berada dalam keadaan diam atau bergerak lurus beraturan apabila resultan gaya yang bekerja pada benda sama dengan nol”.

Secara matematis, Hukum I Newton dinyatakan dengan persamaan:

∑F = 0

Keterangan :

∑F = Resultan gaya (N)

Hukum di atas menyatakan bahwa jika suatu benda mula-mula diam maka benda selamanya akan diam. Benda hanya akan bergerak jika pada suatu benda itu diberi gaya luar. Sebaliknya, jika benda sedang bergerak maka benda selamanya akan bergerak, kecuali bila ada gaya yang menghentikannya. Konsep Gaya dan Massa yang dijelaskan oleh Hukum Newton yaitu Hukum I Newton mengungkap tentang sifat benda yang cenderung mempertahankan keadaannya atau dengan kata lain sifat kemalasan benda untuk mengubah keadaannya. Sifat ini kita ini kita sebut kelembaman atau inersia. Oleh karena itu, Hukum I Newton disebut juga Hukum Kelembaman.

2.2 Hukum II Newton

“Setiap benda yang dikenai gaya maka akan mengalami percepatanyang besarnya berbanding lurus dengan besarnya gaya dan berbanding tebalik dengan besarnya massa benda.”

a = , ∑F = m a

Keterangan :

a = percepatan benda (ms-2)

m = massa benda (kg)

F = Gaya (N)

Kesimpulan dari persamaan diatas yaitu arah percepatan benda sama dengan arah gaya yang bekerja pada benda tersebut. Besarnya percepatan sebanding dengan gayanya. Jadi bila gayanya konstan, maka percepatan yang timbul juga akan konstan Bila pada benda bekerja gaya, maka benda akan mengalami percepatan, sebaliknya bila kenyataan dari pengamatan benda mengalami percepatan maka tentu akan ada gaya yang menyebabkannya. Persamaan gerak untuk percepatan yang tetap yaitu :

V_t = V₀ + at

X_t = X₀ + V₀t + ½ at²

V² = V₀² + 2a(X_t – X₀)

Keterangan :

Vt = kecepatan akhir (m/s)

V₀ = kecepatan awal (m/s)

V = kecepatan (m/s)

Xt = jarak akhir (m)

X₀ = jarak awal (m)

a = percepatan (m/s²)

t = waktu (s)

Jika sebuah benda dapat bergerak melingkar melalui porosnya, makapada gerak melingkar ini akan berlaku persamaan gerak yang ekivalen dengan persamaan gerak linear. Dalam hal ini ada besaran fisis momen inersia (momen kelembaman) I yang ekivalen dengan besaran fisis massa (m) pada gerak linear. Momen inersia (I) suatu benda pada poros tertentu harganya sebanding dengan massa benda terhadap porosnya.

I ~ m

I ~ r2

Dimana harga tersebut adalah harga yang tetap

2.3 Hukum III Newton

Hukum III Newton menyatakan bahwa “Apabila benda pertama mengerjakan gaya pada benda kedua (disebut aksi) maka benda kedua akan mengerjakan gaya pada benda pertama sama besar dan berlawanan arah dengan gaya pada benda pertama (reaksi).” Secara matematis dinyatakan dengan persamaan :

Faksi = – Freaksi

Keterangan :

F = gaya (N)

Suatu pasangan gaya disebut aksi-reaksi apabila memenuhi syarat sebagai berikut :

1.      sama besar

2.      berlawanan arah

3.      bekerja pada satu garis kerja gaya yang sama

4.      tidak saling meniadakan

5.      bekerja pada benda yang berbeda

6.       

2.4 Gerak translasi

Gerak lurus adalah gerak suatu obyek yang lintasannya berupa garis lurus. Dapat pula jenis gerak ini disebut sebagai suatu translasi beraturan. Pada rentang waktu yang sama terjadi perpindahan yang besarnya sama. Gerak lurus dapat dikelompokkan menjadi gerak lurus beraturan dan gerak lurus berubah beraturan yang dibedakan dengan ada dan tidaknya percepatan.

1.      Gerak Lurus Beraturan (GLB)

Gerak lurus beraturan (GLB) adalah gerak lurus suatu obyek, dimana dalam gerak ini kecepatannya tetap atau tanpa percepatan, sehingga jarak yang ditempuh dalam gerak lurus beraturan adalah kelajuan kali waktu.

s = v t

Keterangan :

s = jarak tempuh (m)

v = kecepatan (m/s)

t = waktu (s)

2.      Gerak Lurus Berubah Beraturan (GLBB)

Gerak lurus berubah beraturan (GLBB) adalah gerak lurus suatu obyek, di mana kecepatannya berubah terhadap waktu akibat adanya percepatan yang tetap. Akibat adanya percepatan rumus jarak yang ditempuh tidak lagi linier melainkan kuadratik. Dengan kata lain benda yang melakukan gerak dari keadaan diam atau mulai dengan kecepatan awal akan berubah kecepatannya karena ada percepatan ( a = + ) atau perlambatan ( a = – ) Pada umumnya GLBB didasari oleh Hukum Newton II ( Σ F = m a)

Vt = V0 + at

Vt² = V₀² + 2aS

S = V₀t + a t²

Keterangan:

V0= kecepatan awal (m⁄s)

Vt= kecepatan akhir (m⁄s)

a = percepatan (m⁄ s2)

t = waktu (s)

S = jarak yang ditempuh (s)

GLBB dibagi menjadi 2 macam :

1.      GLBB dipercepat

GLBB dipercepat adalah GLBB yang kecepatannya makin lama makin cepat, contoh GLBB dipercepat adalah gerak buah dari pohonnya.

1.      GLBB diperlambat

GLBB diperlambat adalah GLBB yang kecepatannya makin lama makin kecil (lambat). Contoh GLBB diperlambat adalah gerak benda dilempar keatas.

Persamaan yang digunakan dalam GLBB sebagai berikut :

Untuk menentukan kecepatan akhir

v = v₀ +/- at

Keterangan :

V = kecepatan (m/s)

V₀ = kecepatan awal (m/s)

a = percepatan (m/s²)

t = waktu (s)

Untuk menentukan jarak yang ditempuh setelah t detik adalah sebagai berikut:

s = v₀t +/- 1/2 at²

V = kecepatan (m/s)

V₀ = kecepatan awal (m/s)

a = percepatan (m/s²)

t = waktu (s)

s = jarak (m)

Yang perlu diperhatikan dalam menggunakan persamaan diatas adalah saat GLBB dipercepat tanda yang digunakan adalah (+) . Untuk GLBB diperlambat tanda yang digunakan adalah (-) , catatan penting disini adalah nilai percepatan (a) yang dimasukkan pada GLBB diperlambat bernilai positif karena dirumusnya sudah menggunakan tanda negatif.

Berikut Contoh  Percobaan Atwood :

METODE PERCOBAAN

3.1 Alat dan Bahan

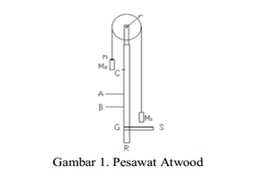
3.1.1 Pesawat Atwood yang terdiri dari (gambar 2).

3.1.1.1 Tiang yang berskala R yang ujung atasnya terdapat katrol p

3.1.1.2 Tali penggantung yang massanya dapat diabaikan.

3.1.1.3 Dua beban M1 dan M2 berbentuk silinder dengan massa sama masing-masing M yang diikatkan menggantung.

3.1.1.4 Dua beban tambahan dengan massa masingmasing m1 dan m2.

3.1.1.5 Genggaman G dengan pegas S, penahan beban B, penahan beban tambahan A yang berlubang.

3.1.2 Stopwatch

3.1.3 Neraca Teknis

3.1.4 Kertas Grafik (milimeter)

3.2 Prosedur

3.2.1 Mengambil alt-alat yang diperlukan.

3.2.2 Menimbang dan mencatat M1 dan M2 serta m1 dan m2.

3.2.3 Memasang genggaman G, penahan beban B dan penahan beban tambahan A.

3.2.4 Menggantungkan M1 dan M2 pada ujung-ujung tali dan memasangkannya pada katrol (lihat gambar 2).Memasang M1 pada genggaman dan menyelidiki apakah tiang sejajar dengan tali.

3.2.5 Setelah tiang sejajar, menekan S dan menuliskan apa yang terjadi dan memberi penjelasan.

3.2.6 Setelah pesawat bekerja dengan baik, memasang M1 pada genggaman G, dan menambahkan m1 dan M2. Mencatat kedudukan C,kedudukan penahan A dan kedudukan penahan B pada tiang berskala.

3.2.7 Melepaskan M1 dari G dengan menekan S. Mencatat tAB, yaitu waktu yang diperlukan oleh M2 (setelah m1 tersangkut pada A) untuk menempuh jarak XAB (=AB).

3.2.8 Mengganti m1 dengan m2, kemudian melakukan percobaan poin 3.2.7.

3.2.9 Mengubah jarak XAB dengan cara mengubah kedudukan B, sedangkan kedudukan Cdan A tetap dan mengulangi poin (3.2.7) dan (3.2.8).

3.2.10 Mengubah lagi jarak XAB dan ulangi percobaan lagi.

3.2.11 Memuat grafik antara XAB terhadap tAB untuk masing-masing beban tambahan m1 dan m2. Bandingkan dengan hukum II Newton.

3.2.12 Dari grafik tersebut,  menghitung kecepatan M2 setelah melalui A untuk masing-masing beban tambahan.

3.2.13 Mengatur kedudukan A, B, C. Sebaiknya CA cukup jauh, sedangkan AB dekat. Catat kedudukan C dan A, pasang M1 pada G dan tambahkan m1 pada M2.

3.2.14 Melepaskan M1 dari G. Catat tCA.

3.2.15 Mengganti m1 dengan m2, lakukan lagi seperti tahap sebelumnya.

3.2.16 Mengubah jarak XCA dengan mengubah kedudukan G. Catat kedudukan C dan lakukan lagi seperti tahap sebelumnya.

3.2.17 Mengubah jarak XCA sekali lagi, catat kedudukan C dan ulangi tahapan sebelumnya.

3.2.18 Membuat grafik antara XCA terhadap tCA 2untuk masing-masing beban tambahan m1 dan m2. Bandingkan dengan hukum Newton.

3.2.19 Dari grafik tersebut,  menghitung percepatan M2 dengan masingmasing beban tambahan.

3.2.20 Hitung momen inersia katrol dari percobaan, jika M2 ditambah m1 dan jika M2 ditambah m2.

SUMBER REFERENSI
Dewi, Rohmatulizza,2015. Pesawat atwood.  Dalam web dewirohmatulizzati.
 Wati,Nurfauzia.2012. Modul 2- Pesawat atwood. Dalam Web Nurfauziawati